Revisitando el concepto de normal (3/6)
El concepto de normal a una primitiva (normal a una recta, normal a un plano) también es algo que debemos volver a repensar, sobre todo en 4D, porque nos vamos a llevar un par de sorpresas.
Comencemos en 2D, donde la normal a una recta es aquella cuyo vector dirección es perpendicular a la primera. La recta original tiene un grado de libertad, y la normal es otra recta con otro grado de libertad, y juntas representan los dos grados de libertad que tiene el espacio 2D. Ambas rectas cortan en un punto donde ambas son normales.
En el espacio 3D, tenemos que la normal a un plano es una recta, y viceversa: la normal a una recta es un plano. La recta tiene un grado de libertad, y el plano está formado por otros dos grados de libertad, que son ambos perpendiculares al vector dirección de la recta. Y de nuevo se cumple que la suma de los grados de libertad de la primitiva y de su normal dan como resultado el número de grados de libertad del espacio 3D.
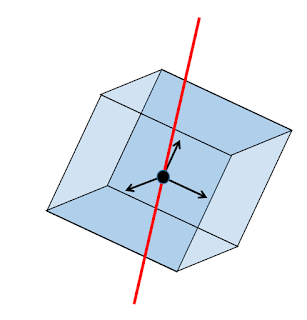
Pero atención ahora que vienen las sorpresas. En el espacio 4D, la normal a un plano, ¿cuál piensan que será? Recordemos lo que pasó anteriormente: la normal a una recta en 2D es otra recta, pero la normal a una recta en 3D es un plano. Hay un grado de libertad más en 3D. Miremos atentamente un caso muy sencillo en 4D: el plano xy.
Si miramos la figura, parece una escena normal en 3D, donde vemos que el vector z es normal al plano. Pero nooooooo. Estamos ya en 4D. Existe un cuarto eje (llamémosle w) que no lo he pintado porque no sé dónde pintarlo!!! Es una cuarta dimensión que sale hacia algún lado, pero que para nosotros resulta imposible de ver, porque vivimos en un mundo de tres dimensiones.
Pero una cosa sí sabemos: ese cuarto eje, w, va a ser ortogonal a los otros tres, x,y,z!!! Es muy difícil imaginarse eso visualmente, pero matemáticamente es trivial. En un espacio 3D, los tres ejes x,y,z vienen dados por las expresiones (1,0,0), (0,1,0), y (0,0,1) respectivamente. Y sabemos que son perpendiculares simplemente porque al realizar el producto escalar entre cualesquiera dos, sale cero. Al pasar a 4 dimensiones, las expresiones para los cuatro ejes, x,y,z,w, tienen la misma forma. Son respectivamente (1,0,0,0), (0,1,0,0), (0,0,1,0) y (0,0,0,1). Y si hacemos el producto escalar para cualquiera dos de ellos, nos vuelve a salir siempre cero, señal inequívoca de que son todos ortogonales entre sí.
Por tanto, es cierto que el vector z es normal al plano: la prueba es que cualquier vector contenido en el plano tiene la pinta (a,b,0,0), y al multiplicarlo por el vector z=(0,0,1,0) siempre sale cero. Pero resulta que el vector w, que está por ahí flotando en esa cuarta dimensión, también es normal al plano!!! En efecto, igual que ocurría con el vector z, cualquier vector contenido en el plano, (a,b,0,0) sale cero cuando lo multiplicamos por el vector w=(0,0,0,1).
Y voy más allá: al ser perpendicular al plano tanto el vector z como el vector w, cualquier combinación de ellos también será normal al plano, puesto que el vector (0,0,c,d) multiplicado por (a,b,0,0) siempre saldrá cero. Luego la normal a un plano en 4D es un elemento que tiene dos grados de libertad, y eso ya vimos antes que es un plano. Por tanto, podemos afirmar que la normal a un plano en 4D es otro plano!!!
Sí, sí, es súper difícil verlo, pero está ahí. No es un invento. Así es el mundo 4D. Y de hecho, era lo esperable. Un plano tiene dos grados de libertad, y su normal debería tener otros dos grados de libertad, para entre ambos sumar los 4 grados de libertad del espacio 4D.
Además ocurre otra propiedad curiosa. En 2D y 3D, todos los elementos y sus normales se cortan en un único punto. Pasaba eso con una recta y su normal en 2D, y pasaba también con un plano y su recta normal en 3D. Pues bien, aquí sigue pasando lo mismo, un plano en 4D y su plano normal se cortan en un único punto (otra propiedad difícil de imaginar). En el ejemplo sencillo que usamos antes, el plano xy original, tiene por ecuación z=w=0 (todos los puntos del plano son los que tienen la z y la w a cero, para cualquier valor de x,y). Y su plano normal es el plano formado por los vectores z,w, con lo cual su ecuación es x=y=0 (formado por todos los puntos que tienen la x y la y a cero, para cualquier valor de z,w). Por tanto, puntos que pertenezcan a ambos planos, y por tanto que verifiquen ambas ecuaciones, solo existe uno: el origen de coordenadas, el punto (0,0,0,0).
En 4D aún nos queda un elemento por hallar su normal: el hiperplano. Si la regla se sigue cumpliendo, un hiperplano, que vimos que tiene 3 grados de libertad, tendrá como normal una recta (1 grado de libertad), y viceversa, para entre ambos sumar los 4 grados de libertad del espacio. Considerando el hiperplano como un volumen, esa recta normal cortará en un único punto al hiperplano (cosa difícil también de ver), y se extenderá a lo largo de esa cuarta dimensión. Acojonante.





Comentarios
Publicar un comentario