Rotación 4D (5/6)
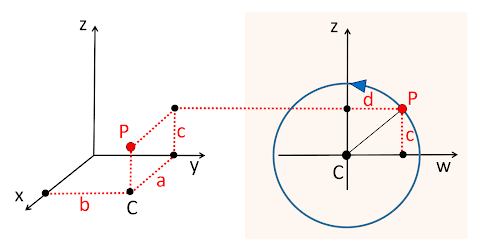
Ya estamos más cerca de ver cómo va a ser esa rotación tan misteriosa en un espacio de 4 dimensiones. Pero antes de eso, necesitamos alguna forma de representar coordenadas en este espacio 4D. Existen varias alternativas, pero yo voy a usar una que me parece la más fácil de entender. La representación la dividimos en dos vistas: a la izquierda, una representación clásica del sistema 3D para los ejes x,y,z; y a la derecha, una vista plana de los ejes z y w.
De esta forma, un punto cualquiera, P=(a,b,c,d), se representa a la izquierda de forma clásica (desplazando las distancias a,b,c en cada eje) y luego las coordenadas z,w se representan a la derecha (desplazando las distancias c,d en cada eje). Tenemos que tener en cuenta que el eje w está flotando ahí, en la figura de la izquierda, mezclado con los otros tres, y cruzando de forma ortogonal por el origen, pero no lo vemos. Está en otra dimensión, y por eso nos abstraemos y lo pintamos sólo en la parte derecha para aclararnos. En esta representación, los movimientos a lo largo de los ejes x,y sólo se verán en la figura izquierda, los movimientos verticales en z se verán en ambas figuras a la vez, y los movimientos en w sólo se verán a la derecha.
Por tanto, ya estamos en disposición de plantear una rotación en 4D. Cojamos por ejemplo el punto P anterior que hemos representado, y digamos que queremos rotarlo alrededor del plano xy. Ya sé que es muy muy difícil de imaginarlo, pero con lo que hemos hablado en los post anteriores, podemos deducir varias cosas:
- la órbita del punto P al girar va a estar contenida en un cierto plano (al igual que sucedía en 3 y 2 dimensiones)
- el plano que contiene a la órbita de P debe ser normal al plano xy (con respecto al cual estamos rotando)
- dentro de ese plano normal, habrá un punto C alrededor del cual P está girando
- este punto C será el punto del plano xy más cercano al punto P
Estos hechos se ven claramente en una rotación 3D como la del post anterior (vuelvo a mostrar la figura):
Si cambiamos el término "plano xy" por "eje de rotación" vemos que las cuatro condiciones anteriores se cumplen perfectamente. Pues ahora extrapolemos esto a nuestro sistema 4D, a ver qué obtenemos.
En primer lugar, si atendemos a la última condición, el punto C es sencillo ver dónde está. Si es el punto del plano xy más cercano al punto P, entonces C es simplemente la proyección de P sobre el plano xy. Podemos verlo en la figura siguiente.
En la vista izquierda se ve claro que C es el punto del plano xy más cercano a P. Como C descansa en el plano xy, démonos cuenta que la ecuación del plano xy es z=w=0; es decir, este plano está formado por todos los puntos con cualquier valor de x y de y (dos grados de libertad) donde la altura de z y de w es cero. Por tanto, realmente las coordenadas de C son (a,b,0,0), y es por esto que en la vista del plano zw, C aparece en el origen.
Fijémonos también que en la vista derecha de la figura, aunque veamos de fondo el plano zw, cuya ecuación es x=y=0, los puntos C y P no están en el plano x=y=0 sino en el plano {x=a; y=b}, que es paralelo al plano zw, pero se encuentra a otra altura de las coordenadas x,y. Este plano {x=a; y=b} contiene a C y a P, y es normal al plano xy (z=w=0). Y además, ambos planos se cortan justo en el punto C=(a,b,0,0).
Por tanto, uniendo todas las condiciones, ya podemos representar la órbita que va a seguir el punto P al rotar sobre el punto C en el plano {x=a; y=b}.
Paremos un momento a pensarlo. Es complicado de ver. Pero matemáticamente está ahí. Es simple. Todas las ecuaciones cuadran. Pero a nuestra mente le cuesta visualizarlo, porque nuestra mente sólo sabe moverse en el espacio 3D. Y sin embargo, P está dando vueltas, manteniendo fija la distancia hasta el punto C, y sin tocar nunca el plano xy.
Con nuestra visión 3D, en la figura izquierda lo que ocurrirá es que veremos al punto P subir y bajar en la vertical que mantiene con C, y parecería que está atravesando el plano xy, pero no es así realmente, porque el movimiento en la dirección w hace que siempre estemos a la misma distancia de C, y por tanto ni nos acercamos ni nos alejamos de él.



Comentarios
Publicar un comentario