Es normal que nos cueste verlo. Si es la primera vez que estamos imaginando la cuarta dimensión, es como la primera vez que nos enfrentamos a aquellos libros de imágenes estereográficas, que había que concentrarse y dejar los ojos mirando hacia el infinito para lograr que aquellas imágenes extrañas pintadas en 2D, de repente cobraran tridimensionalidad en nuestra cabeza. No era fácil. Pero si lográbamos concentrarnos y hacer un esfuerzo mental, conseguíamos verlo.
Pues esto es parecido. Hay que abrir la mente, y concentrarse.
Y para lograr esta concentración, tenemos una ayuda enorme en la fábula de Flatland que nos contaba en el primer post Carl Sagan. Porque podemos sentir y entender la dificultad de los habitantes del mundo 2D Flatland al intentar explicarles cómo es una rotación 3D. Y esa misma frustración que ellos podrían sentir al tratar de entenderla, es exactamente la misma que nos pasa a nosotros para entender una rotación 4D.
Pongámonos en la mente de un habitante de Flatland. Sólo conoce 2 dimensiones, el plano xy donde vive. Está acostumbrado a rotar un punto P alrededor de otro punto C, siempre en el plano. Y al rotar, mantiene la misma distancia hasta el punto C durante toda la órbita.
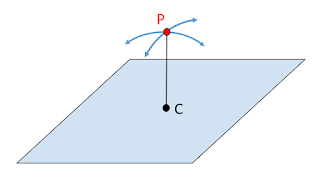
Pero ahora le decimos que intente visualizar la tercera dimensión, y que en lugar de rotar alrededor de un punto vamos a rotar alrededor de una recta. ¿Qué pensará nuestro amigo? Él tenderá a pintar una recta en el plano (puesto que son las únicas rectas que conoce), pintará el punto P, y se preguntará: ¿cómo carajo se orbita alrededor de una recta? ¿Para dónde muevo el punto P?
Pensará que es imposible. No se puede rotar alrededor de la recta. Él puede entender que el punto más cercano a la recta es C. Pero es imposible rotar alrededor de C sin atravesar la recta. No hay forma humana de hacerlo. Y se rendirá.
Pero entonces, hay que explicarle que existe una tercera dimensión, z, perpendicular a las dos que ya conoce, y que simplemente abriendo la mente e imaginando que ésta existe, puede usarla para desplazar el punto P a lo largo de esa dimensión y orbitar alrededor del punto C para caer al otro lado de la recta sin tocarla!!
Para nosotros es super obvio, pero para nuestro amigo de Flatland le va a costar muchísimo.
Pues bien, exactamente nos ocurre lo mismo a nosotros. Exactamente. Nos dicen que vamos a rotar un punto alrededor de un plano, y no lo entendemos, porque pintamos un plano en 3D (digamos el plano xy), pintamos el punto P, llegamos incluso a pintar el punto C perteneciente al plano xy que más cercano se encuentra de nosotros, pero no sabemos cómo rotar. ¿Hacia dónde lo movemos? Nos parece imposible. ¿Cómo girar alrededor del punto C sin acercarnos al plano? ¿Cómo vamos a llegar al otro lado del plano sin atravesarlo? Es imposible!!!!! Son exactamente las mismas preguntas que nuestro amigo de Flatland se hacía antes. Las mismas.
¿Y cuál es la respuesta a nuestras preguntas? Pues algo super obvio para una criatura del espacio 4D. Abre tu mente. Siente la cuarta dimensión adicional, w, que es perpendicular a las tres que conoces. Está ahí, flotando. Esta nueva dimensión sale del punto C y apunta en una dirección que es normal al plano xy, pero también normal al eje z. Imagínala.
Y entonces, puedes ver que esa cuarta dimensión forma un plano con la dirección z (dos grados de libertad), y ese plano entero es normal al plano xy. Y si mueves el punto P en ese plano, conseguirás orbitar alrededor del punto C sin tocar el plano xy!!
Recuerda. Es como el libro de los estereogramas. No lo vas a conseguir visualizar la primera vez, ni la segunda, pero créeme que la rotación existe, está ahí, esperando que la encuentres y la puedas ver. Ten paciencia, y buena suerte.
Comentarios
Publicar un comentario