Rotaciones en 2D y 3D (4/6)

Bien. Si has llegado hasta aquí, entonces es que tienes curiosidad por saber cómo es eso de rotar alrededor de un plano. Vamos a irlo desgranando entonces hasta poder visualizarlo.

Empecemos en 2D, donde tenemos claro cómo es una rotación. Cuando rotamos un punto P alrededor de un punto C, ocurre que P da vueltas en torno a C, manteniendo siempre la misma distancia entre ambos puntos. Esto significa que P, a medida que gira, siempre se encontrará sobre la circunferencia de centro C y radio la distancia entre P y C. Podemos decir que en la rotación hay un único grado de libertad que podemos variar, que sería el ángulo a rotar.

Pasemos ahora a 3D. En un espacio de tres dimensiones, la rotación más sencilla no es alrededor de otro punto, sino de una recta (eje). Esto es así porque, si rotáramos un punto P alrededor de un punto C central, no tendríamos un único grado de libertad como antes, sino que habría dos. Para verlo, pensemos que esta vez P giraría en el espacio alrededor de C, manteniendo siempre la misma distancia entre ambos puntos. Por tanto, P no estaría sobre una circunferencia sino sobre una esfera. El ejemplo más fácil es considerar el planeta Tierra como una esfera con centro en C, y al rotar el punto P alrededor del centro tenemos dos grados de libertad, que son dos ángulos, llamados latitud y longitud.
Por eso, vamos a considerar la rotación en 3D alrededor de un eje, que es más sencilla. En este caso, el eje de rotación es una recta en el espacio, y el punto P gira alrededor de dicho eje. Vuelve a haber sólo un único grado de libertad. Mientras gira, el punto P siempre mantiene la misma distancia hasta el eje. Si llamamos C al punto de la recta más cercano al punto P, tenemos que P durante su giro traza una circunferencia centrada en C, y contenida en el plano perpendicular al eje que pasa por C. Precisamente este plano es la normal a la recta que contiene a P.
Por ejemplo, cojamos un caso más fácil de ver. Supongamos que queremos rotar el punto P=(1,1,1) alrededor del eje z. El punto del eje de rotación más cercano a P es el punto C=(0,0,1), es decir, el punto del eje que está a la misma altura que P sobre el suelo. Y la órbita que hará P al rotar será un círculo de radio raiz(2) sobre el plano z=1, que es el plano que contiene a C y es perpendicular (normal) al eje z.
Si nos fijamos bien, considerando el plano que contiene a la órbita de la rotación, volvemos a estar en el mismo caso que en la rotación 2D: hay un punto C, que es el punto del eje de rotación más cercano a P, y P realiza una rotación 2D alrededor de C en ese plano. Esta forma de verlo va a ser muy importante, porque va a ocurrir lo mismo cuando demos el salto a 4D: el punto P va a girar de forma circular dentro de un plano en torno a un cierto punto C que ya obtendremos.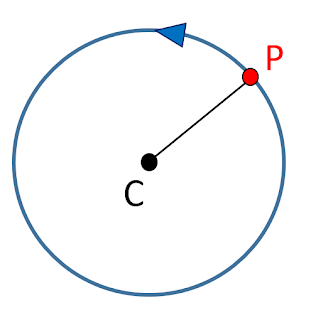

Comentarios

Publicar un comentario

Entradas populares de este blog

Tratando de imaginar la geometría del 4D (1/6)

Imagen
Vivimos en un mundo 3D. Y matemáticamente podemos trabajar con conceptos geométricos básicos que nos resultan sencillos. Conocemos  las ecuaciones de los puntos, rectas y planos, que son los elementos básicos de la geometría. Y además sabemos representarlos y visualizarlos perfectamente. Sabemos cómo hacer para desplazar estos elementos, para escalarlos, y para rotarlos. Lo curioso es que matemáticamente, al igual que podemos pasar de 2D a 3D simplemente añadiendo una tercera coordenada al valor de los puntos, también podemos hacer lo mismo fácilmente para saltar al 4D (4 dimensiones), pero el problema aquí radica en lo complicadísimo que resulta imaginarse este espacio.  Si no has visto el famoso vídeo Flatland de Carl Sagan , te aconsejo verlo. Hace un símil precioso de cómo sería explicarle cómo es un espacio de tres dimensiones a seres que vivieran en un mundo 2D, y que sólo conocieran las direcciones izquierda y derecha, adelante y atrás, pero que no son capaces de imagin...
Leer más

Las primitivas básicas: punto, recta, plano, .... hiperplano! (2/6)

Imagen
En una dimensión, donde solo existe el eje x, el único elemento es el  punto , x=a, donde a es un valor real. Por ejemplo, x=0, que es el punto que se encuentra en el centro de la recta real. Casualmente, este punto separa en dos la recta: deja a un lado los puntos de la izquierda (x<0) y al otro lado los puntos de la derecha (x>0) En 2D pasamos a tener dos ejes, x,y. Ahora un punto ya tiene dos coordenadas, P=(x,y), y una  recta  es una línea que une dos puntos y se extiende hasta el infinito. Al igual que el punto en una dimensión separaba el espacio 1D en dos mitades, ocurre lo mismo en 2D: una recta corta el espacio 2D en dos mitades, una a cada lado de la recta. Estamos acostumbrados a ver una recta con la ecuación explícita y=ax+b, donde a es la pendiente de la recta, y b es el corte de la recta con el eje vertical. Pero esta forma de representación tiene sus desventajas. Por ejemplo, no puedes representar una recta vertical, como por ejemplo x=5. Así que es p...
Leer más

Rotación 4D (5/6)

Imagen
Ya estamos más cerca de ver cómo va a ser esa rotación tan misteriosa en un espacio de 4 dimensiones. Pero antes de eso, necesitamos alguna forma de representar coordenadas en este espacio 4D.  Existen varias alternativas, pero yo voy a usar una que me parece la más fácil de entender. La representación la dividimos en dos vistas: a la izquierda, una representación clásica del sistema 3D para los ejes x,y,z; y a la derecha, una vista plana de los ejes z y w.  De esta forma, un punto cualquiera, P=(a,b,c,d), se representa a la izquierda de forma clásica (desplazando las distancias a,b,c en cada eje) y luego las coordenadas z,w se representan a la derecha (desplazando las distancias c,d en cada eje). Tenemos que tener en cuenta que el eje w está flotando ahí, en la figura de la izquierda, mezclado con los otros tres, y cruzando de forma ortogonal por el origen, pero no lo vemos. Está en otra dimensión, y por eso nos abstraemos y lo pintamos sólo en la parte derecha para aclararno...
Leer más